FIS usage and Defuzzification

NAVIGATION

• Summary : Users guide
• Previous page : Learning rules from data
• Next page : Density information

---

Page content:

1. Sample code
2. Inference process
3. Parameters
4. Defuzzification

---

Once you have completely defined FIS (i.e., output fuzzy partition, inputs partition, and rules are defined), you can use it in production. You can programmaticaly do this in your code, but you can also load a previously saved fis.

Sample code

Using it in production means computing an output value, given a set of input values.

int main()
{
        SLIFIS fis;
        fis.Load( "myfis.fis" ); // this will throw an error if file not found.

// give input values
        fis.SetInputValue( 0, ... ); // one line for each input
        fis.SetInputValue( 1, ... );
        ...

// compute crisp output value
        REALVAL out_val = GetOutputValue( out_val );
        cout << "output value = " << out_val << endl;
}

Inference process

Internally, the FIS takes in charge the required following steps, usually called "fuzzy logic inference". The first step is common to Mamdani and TS Fis. It computes the "firing strength of each rule", that is, how much the given set of input values trigger the rule. The output is a crisp value.

Firing strength of a rule

See Firing strength of a rule

Mamdani inference

For a Mamdani Fis type, the inference process is done is SLIFIS::P_Evaluate_M(). It can be described by the following algorithm:

1. For each rule:
   1. compute the firing strength of the rule;
   2. compute output of the rule (membership function) using implication method;
   3. group together each membership function produced by each rule into a global output membership function, using aggregation s-norm;
2. compute the defuzzyfied value from the global output membership function.

Takagi-Sugeno inference

For a TS type Fis, the inference process is done in SLIFIS::P_Evaluate_TS(). It can be described by the following algorithm:

1. For each rule:
   1. compute the firing strength of the rule;
   2. compute the output value of the rule, using its TS coefficients;
2. group together all the ouputs of all the rules, using weighted average.

For example, say we have for a 2-input fis these two rules:

r_1: IF x1 is "red" AND x2 is "good" THEN y = 2 x1 + 3 x2
r_2: IF x1 is "blue" AND x2 is "bad" THEN y = 3 x1 + 4 x2

Say we have 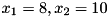, and the membership functions ot the two inputs are defined such that the firing strength of the rules have the following values:

• 
• .

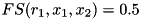
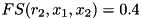Then, we can compute for each rule an output value:

• For rule 1:
• For rule 2:

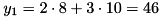
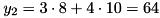
The global output value will be computed as the weighted average of the two ouput values:

Parameters

At each step of this inference process, several parameters can be adjusted:

Each rule uses either the "OR" or the "AND" operation for term aggregation. For "AND" operation, any t-norm among slifis::EN_TNORM can be used, and for "OR" operations, any s-norm amont slifis::EN_SNORM can be used. These can be adjusted by a call to SLIFIS::SetRuleInferenceMethod().

The inference parameters can be edited with the SLIFIS::GetInferenceParams() by assigning values to the INF_PARAMS struct, such as in the following example:

        fis.GetInferenceParams().DefuzzMethod = DF_COG;

It can also be printed out:

        fis.GetInferenceParams().Print( stderr );

Defuzzification

Defuzzification is the operation of computing a crisp value given some membership function. This is required in the Mamdani inference process, that computes a global membership function produced by merging together the output of each rule. Defuzzification requires that the function is finite (i.e. it has left and right zero values). This can be checked by a call to MEMBFUNC::IsFinite().

Actually, the following methods are implemented (the most common), through slifis::EN_DEFUZZMETHOD:

• Maximum (MAX),
• Center of Gravity (COG),
• Center of Area (COA),
• Mean of Maximums (MEMAX),
• Weighted Mean of Maximums (WMEMAX).

See MEMBFUNC::Defuzzify() for details, and demo app demo3.cpp, in folder src/demo.

For a fis, this is done automatically by SLIFIS::GetOutputValue().

---

NAVIGATION

• Summary : Users guide
• Previous page : Learning rules from data
• Top of page : FIS usage and Defuzzification
• Next page : Density information