Membership Functions

NAVIGATION

• Summary : Users guide
• Previous page : Basic data types
• Next page : Sets of membership functions

---

Page content:

1. Introduction
2. Editing a function
3. Operations on membership functions

---

Introduction

The MEMBFUNC class holds a membership function, that defines what is called a "fuzzy set". In this library, membership functions can be defined only by line segments, aka piecewise linear function.

A function has a name, and always has a maximum and minimum value. It can be empty (0 points), but that does not mean it has a null value.

A copy-constructor is provided, as well as an assignement operator and comparison operators ("==" and "!=" ).

Creation and destruction of a membership function

Several constructors are provided to build membership functions, but you can afterwards redefine any function using one of the "Set()" functions. Actually, this is what the constructors do. In the following example, we'll use one or another of these.

For example, you can create an empty function, then assigning to it a name, then assigning to it a predefined shape:

        MEMBFUNC mf;
        mf.SetName( "cold" );
        mf.Set( MF_HL, 10, 20 );

which is strictly identical to:

        MEMBFUNC mf( "cold" );
        mf.Set( MF_HL, 10, 20 );

which in turn is strictly identical to:

        MEMBFUNC mf( MF_HL, "cold", 10, 20 );

You can also assign a constant fuzzy value to a function, with the code:

        MEMBFUNC mf;
        mf.Clear( 0.3 );

which is equivalent to:

        MEMBFUNC mf( 0.3 );

(Here, the function will be assigned a default name).

The MEMBFUNC::Clear() function removes all the points, and assigns the constant value to the function (0 is the default value).

Instanciation of predefined non-symmetric membership function

Five predefined functions are available, through constructors and the enum slifis::EN_MF_TYPE :

1. MF_HL : High to Low (2 points needed)
2. MF_LH : Low to High (2 points needed)
3. MF_LL : Low to Low, with a "1" plateau (4 points needed) (trapezoidal function)
4. MF_TRI : Triangular LHL function, same as the trapezoidal function but only one point at "1" level
5. MF_GAUSS : bell function, approximation of a fuzzy Gaussian function using 7 points.

These will produce classical "0 to 1" functions:

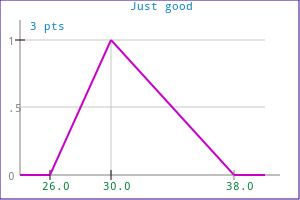
        MEMBFUNC mf1( MF_HL, "cold", 10, 20 );
        MEMBFUNC mf2( MF_LH, "hot", 40, 70 );
        MEMBFUNC mf3( MF_LL, "warm", 20, 40, 50, 60 );
        MEMBFUNC mf4( MF_TRI, "Just good", 26, 30, 38 );

Instanciation of predefined symmetric membership function

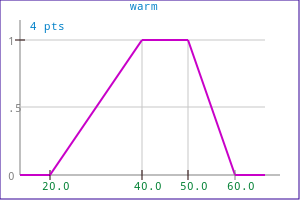
Several symmetric functions can be automatically defined:

• triangular
• trapezoidal
• gaussian ("bell" function)

The triangular function can be defined by only two values, the center value, and its half-width at bottom. For example, the following code:

        mf.Set( MF_TRI, 30.0, 4.0 );

will assign to mf a triangular function centered at 30 with a total width of 8.

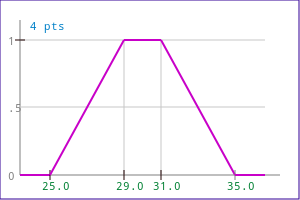
A symmetric trapezoidal function can be defined by giving three values:

• the center value,
• the half width at top (y=1),
• the half width at bottom (y=0).

For example:

        mf.Set( MF_LL, 30.0, 1.0, 5.0 );

Of course, the second and third value must be positive, and the third value must be higher than the second value.

symmetric MF_TRI function	symmetric MF_LL function

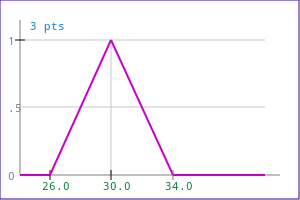
The Gaussian membership function is an approximation of the real function using 6 line segments. It has a 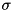("sigma") argument, but contrarly to a real Gaussian, it always has a maximum value of 1.

        MEMBFUNC mf( MF_GAUSS, "Gaussian", x0, sigma );

Although the function may seem a really rough approximation, it is actually not that far from the real Gaussian function, see Gaussian function approximation.

Approximation of a Gaussian function with sigma=0.5, 1, 2, 5

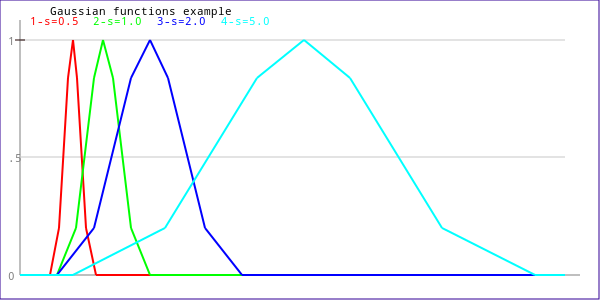
This set of membership function has been generated with this code, from file src/demo/gui/generate-doc-plots.cpp:

                MEMBFUNC fa( MF_GAUSS, "s=0.5", 10.0, 0.5 );
                MEMBFUNC fb( MF_GAUSS, "s=1.0", 12.0, 1.0 );
                MEMBFUNC fc( MF_GAUSS, "s=2.0", 15.0, 2.0 );
                MEMBFUNC fd( MF_GAUSS, "s=5.0", 25.0, 5.0 );
                FUZZY_IN set( "Gaussian functions example" );
                set.AddMf( fa );
                set.AddMf( fb );
                set.AddMf( fc );
                set.AddMf( fd );

Fetching information about a function

Several functions are provided to give the user some information about the function:

• MEMBFUNC::GetName()
• MEMBFUNC::GetNbPoints()
• MEMBFUNC::GetLeftValue()
• MEMBFUNC::GetRightValue()
• MEMBFUNC::GetMaxValue()
• MEMBFUNC::GetMinValue()
• MEMBFUNC::IsEmpty()
• MEMBFUNC::IsNull()
• MEMBFUNC::IsFinite()
• MEMBFUNC::IsValid()

Fuzzyfication of a real value

Once you have set up a MF, its goal is to give you the fuzzy value corresponding to a real value. This is done with the MEMBFUNC::Fuzzify() function.

        REALVAL x;
        ...
        FUZZYVAL y = mf.Fuzzify( x );

Editing a function

Adding points one by one

You can create an empty function and add points one by one, by giving x and y values with MEMBFUNC::AddPoint() :

        MEMBFUNC mf1("warm");
        mf1.AddPoint( 20, 0 );
        mf1.AddPoint( 30, 1 );
        mf1.AddPoint( 40, 1 );
        mf1.AddPoint( 60, 0 );

Remarks:

What happens if you type the following code ?

        mf1.AddPoint( 20, 2 );

No problem! due to the way the constructor for FUZZYVAL is written, the fuzzy value will be truncated to 1. Be warned however that no warning will be issued.

Warning:

Remember that to be valid, a function must be either empty, or have at least two points. Leaving a function with only one point will trigger an error later on.

Editing points

Editing a membership function can be done by modifying its points, assuming you know their indexes, with the function MEMBFUNC::ModifyPoint() :

        mf.ModifyPoint( idx, 30, 0.5 );

or

        FPOINT new_point( 30,  0.5 );
        mf.ModifyPoint( idx, new_point );

Most of the time, you only need to change the fuzzy value of the point, you can do that directly:

        mf.ModifyPoint( idx, 0.4 );

Or you can also remove it, with MEMBFUNC::DeletePoint(), and add the new point:

        mf.DeletePoint( idx );
        mf.AddPoint( FPOINT( 30,  0.5 ) );

Don't worry about the order of points inside the membership function, they will be correctly reordered inside automatically.

You can also shift the whole function left or right, using MEMBFUNC::Shift() :

        mf.Shift( 2.0 ); // shifts all the points to right (+2)

If you want to clear a function and make it empty, just use the MEMBFUNC::Clear() :

        mf.Clear();

This function can also be used to assign some constant value to a function (indeed, a function can have no points without having a null value).

        mf.Clear( 0.3 );

Operations on membership functions

Two types of operations can be done with membership functions (aka "fuzzy sets"), unary operations and binary operations. Unary operations are implemented as self-transforming (non-const) member functions, i.e., they are in the form:

        MEMBFUNC mf;
         ... // add content
        mf.DoThis();

while binary operation are implemented as free functions, in the form:

        DoThis( mf1, mf2, mf_result );

Unary operations

The following unary operations are available:

• Alphacut: MEMBFUNC::AlphaCut()
• Truncate: MEMBFUNC::Truncate()
• Scale: MEMBFUNC::Scale()
• Complement: MEMBFUNC::Complement()

For a quick example, see the following code and the generated functions:

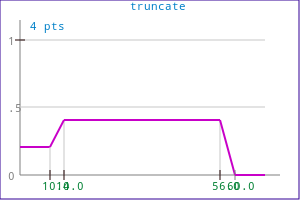
        MEMBFUNC mf( MF_LL, "test", 10, 20, 50, 60 );
        mf.ModifyPoint( 1, 0.7 );
        MEMBFUNC mf_T(mf);
        MEMBFUNC mf_A(mf);
        MEMBFUNC mf_C(mf);

        mf_T.Truncate(0.4);
        mf_A.AlphaCut(0.4);
        mf_A.Scale(0.4);
        mf_C.Complement();

Original function	Complement
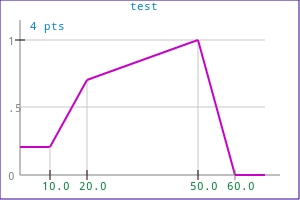
Alphacut (0.4)	Truncate (0.4)	Scale (0.4)

Binary operations

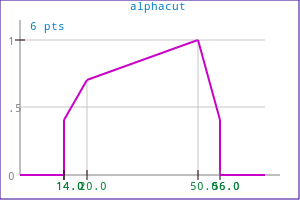
Binary operations are called in the litterature t-norms and t-conorms. See the following links for details:

• http://en.wikipedia.org/wiki/T-norm.
• http://www.scholarpedia.org/article/Triangular_norms_and_conorms

These norms map to slifis::EN_TNORM and slifis::EN_SNORM used for the inference process (see FIS usage and Defuzzification), and slifis::EN_MERGE_OP holds both. At present, the following are supported:

• t-norms
  • product (OPM_PRODUCT):
  • min (OPM_MIN):
  • Łukasiewicz t-norm (OPM_LUKAS): ( )
• t-conorms
  • max (OPM_MAX):
  • Probabilistic sum (OPM_PSUM):
  • Bounded sum (OPM_BSUM):

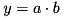
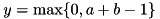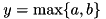
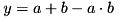
Either you call the function FuzzyMerge(), with the appropriate slifis::EN_MERGE_OP value as argument, or you can directly call one of the following:

• FuzzyMax()
• FuzzyMin()
• FuzzyProduct()
• FuzzyBSum()
• FuzzyPSum()
• FuzzyLukas()

These functions are declared in global_functions.hpp and implemented in global_functions.cpp.

Examples of binary merging operations

See below examples of these binary operations:

• MAX operation examples
• MIN operation examples
• PRODUCT operation examples
• PSUM operation examples
• BSUM operation examples
• LUKAS operation examples

MAX operation examples

The OR operation is achieved with the following code:

FuzzyMax( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_MAX, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

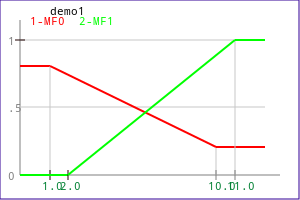
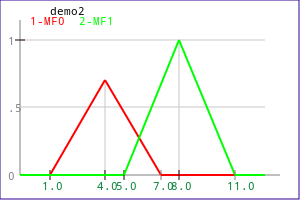
Example 2:

Source functions	Corresponding output function

MIN operation examples

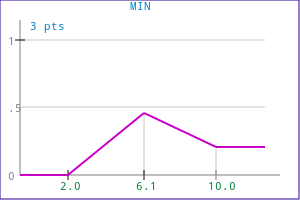
The MIN operation is achieved with the following code:

FuzzyMin( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_MIN, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

Example 2:

Source functions	Corresponding output function

PRODUCT operation examples

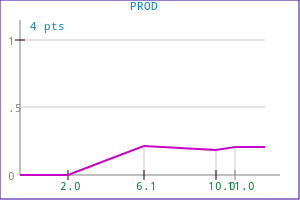
The product operation is achieved with the following code:

FuzzyProduct( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_PRODUCT, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

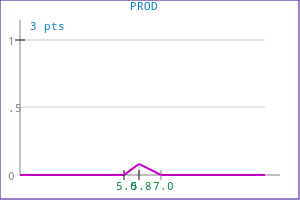
Example 2:

Source functions	Corresponding output function

PSUM operation examples

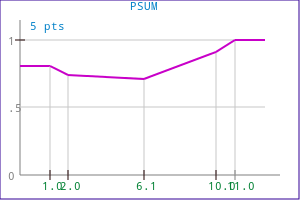
The probalistic sum operation is achieved with the following code:

FuzzyPSum( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_PSUM, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

Example 2:

Source functions	Corresponding output function

BSUM operation examples

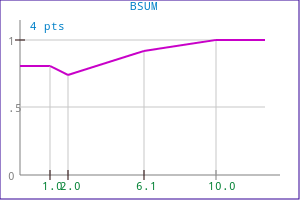
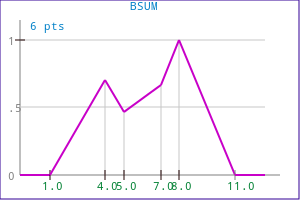
The bounded sum operation is achieved with the following code:

FuzzyBSum( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_BSUM, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

Example 2:

Source functions	Corresponding output function

LUKAS operation examples

The Łukasiewicz t-norm operation is achieved with the following code:

FuzzyLukas( mf0, mf1, mf_out );

or

FuzzyMerge( OPM_LUKAS, mf0, mf1, mf_out );

Example 1:

Source functions	Corresponding output function

Example 2:

Source functions	Corresponding output function

---

NAVIGATION

• Summary : Users guide
• Previous page : Basic data types
• Top of page : Membership Functions
• Next page : Sets of membership functions