 |
A fuzzy logic C++ library
|
 |
A fuzzy logic C++ library
|
On this page, miscellaneous information that for the moment doesn't fit elsewhere...
Content
This term can have two different meanings, we can have the firing strength of an input related to a membership function, or we can have the firing strength of a rule, given a set of input values. This latter meaning is used for Takagi-Sugeno inference.
This is about how much a given input value "triggers" a membership value. For example, if we have an input with an associated set of two triangular membership function such as the following:
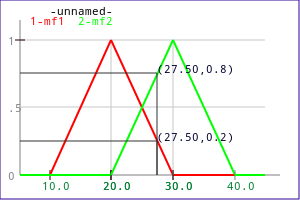
If the input value is, for example 27.5, then the membership function mf1 will be triggered with a (fuzzy) value of 0.2, and the membership function mf2 will be triggered with a value of 0.8.
This can be used when plotting a 2-input rule base (class slifis_plot::PLOT_RB_2D), to visually show how much the input triggers the input functions.
Related functions:
This is about the firing strength of a rule, expressed as a fuzzy value, for some input values. It can be defined by the degree to which the antecedent part of a fuzzy rule is satisfied. It is also known as "degree of fulfillment" in some sources. Its computation depend on the rule operator:
It works as follow, for a rule r:
For example, for a given "AND" rule, and using the (default) product t-norm
if input-1 is "blue" and input-2 is "hot" and input-3 is "nice", then output is ...
If input-1 triggers the "blue" membership function with a value of 0.9, input-2 triggers the "hot" membership function with a value of 0.8, and input-3 triggers the "nice" membership function with a value of 0.4, then the Firing strength of the rule will be 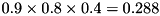
Related functions:
In order to print human readable strings from enumerations values, all the enum types have an associated GetString() function.
Usage: say you have an enum value enum_val of type EN_ENUMTYPE, and you want to print out its value in a human-readable form:
EN_ENUMTYPE enum_val;
enum_val = ...; // some value
cout << "enum_val = " << GetString(enum_val) << endl;
Additionally, the following function are also related, although they have no argument:
The library provides an approximation of a Gaussian function using 6 line segments (3 per side). Each segment approximates a part of the Gaussian function 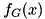 . For a centered (
. For a centered ( 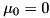 ) function, the segments are computed as follows:
) function, the segments are computed as follows:
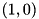 to
to 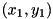 , with
, with 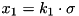 and
and 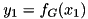
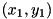 to
to 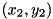 , with
, with 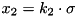 and
and 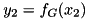
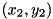 to
to 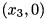 , with
, with 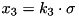
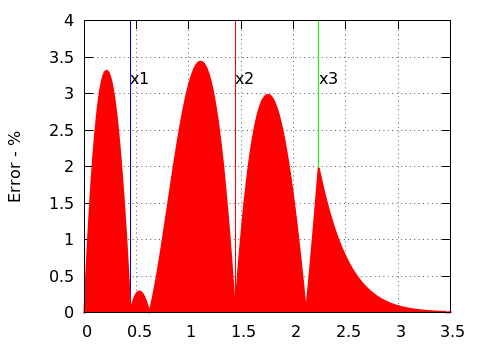
The values 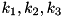 are at present arbitrary chosen to produce something that looks ok. The corresponding error can be plotted with the gnuplot script file misc/GaussianError.plt, that produces the following plots. Absolute error will be less than 3% most of the time.
are at present arbitrary chosen to produce something that looks ok. The corresponding error can be plotted with the gnuplot script file misc/GaussianError.plt, that produces the following plots. Absolute error will be less than 3% most of the time.
| Real Gaussian compared to approximation | Absolute error (adapted scale) |
|---|---|
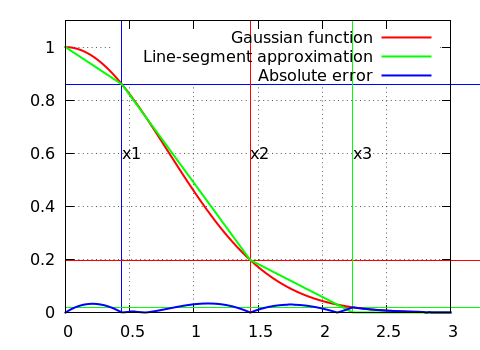
| 
|
See also:
 1.7.6.1
1.7.6.1